Roche Limiti
Roche Limiti bir gökcisminin, çevresinde döndüğü gökcismine dağılmadan yaklaşabileceği minimum mesafeyi belirtir.

Gezegeninin etrafında dönmekte olan bir uydumuz olsun, uydumuz gezegenine yaklaştıkça, gezegene yakın kısımları ile gezegene uzak olan diğer kısımlar arasında kütle çekim farkı oluşur. Bunu yer çekimi gücünün uzaklığın karesiyle ters orantılı olduğu gerçeğinden de çıkarabiliriz.
Oluşan bu kütle çekim farkı uyduyu dağılmaya zorlar fakat bu kütle çekim farkını uydunun kendi yer çekimi engellemeye çalışır. Yer çekimi içe doğrudur ve uydunun bütünlüğünü korumakla mükelleftir.
Uydunun kendi yer çekiminin, bütünlüğünü koruyabildiği son sınır Roche Limiti adını verdiğimiz parametredir.

Roche Limiti aşılacak olur ise uydunun gezegene yakın olan kısmı aşırı bir çekim gücüne maruz kalacak, kendi yerçekimi gücüde bütünlüğünü korumaya yetmeyeceği için uydu parçalanacak, parçalanan uydunun malzemeleri ise gezegenin yörüngesi etrafında bir yol izleyerek halka oluşturacak. Bu noktada gezegenlerin halkalarını açıklamada roche limitinin kullanıldığı çıkarımınıda rahatlıkla yapabiliriz.
Olayı kavramak için gezegen-uydu örneği üzerinden gittik fakat bu bir yıldız-gezegen sistemi yahut gezegen-kuyruklu yıldız ikilemleri için de geçerlidir. Nede olsa bize gereken bir büyük kütle bir de onun yörüngesi dahilinde olabilen küçük bir kütledir bu kütleler için gezegen, yıldız, uydu, kuyruklu yıldız kavramları fark yaratmaz.

Kuyruklu yıldız-gezegen ikilisinden bir örnek verecek olursak Jüpitere çarpmadan önce 1992 yılında roche limiti dahilinde Shoemaker-Levy 9 adlı kometin parçalanmasını söyleyebiliriz. Jüpiterden kaynaklanan çekim gücü daha komet gezegene çarpmadan onu parçalamıştır.
Halkalı gezegenlerin halkalarının oluşumunu roche limiti ile açıkladığımızı söylemiştik, eğer bizimde çevremizde bize yaklaşan bir uydumuz olsaydı, dünyamız onu parçalayıp kendine bir halka oluşturabilirdi.

Roche Limiti için yaklaşık olarak saptanan matematiksel bağıntı d=2,4228 Rg (ρg /ρu)1/3 şeklindedir buradaki d uzaklık, Rg gezegenin yarıçapı, ρg gezegenin yoğunluğu, ρu uydunun yoğunluğu kavramlarını karşılar. Tabi ki bu bağıntı yaklaşıklık ifade eder sebebi ise formülde uydu ve gezegenin kimyasal ve fiziksel yapısı ihmal edilmiştir.
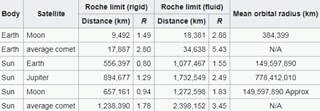
Tabloda belirli gök cisimleri arasında uygun olan roche limitleri gösterilmiştir. Katı ve akışkan olarak ayrılmasının sebebi akışkan bir kütlenin kütle çekimsel gel-gitlere karşı toleransının daha düşük olduğunu göstermek. Ayrıca çevresinde dönülmekte olan bir gök cisminin kütlesi ne kadar fazla ise çevresinde dolanan cismin parçalanmaması için gerekli olan mesafede kat kat fazla hale gelir yani roche limiti için d yükselir.
Bu parametreyi, 1847 yılında Fransız matematikçi Edouard Albert Roche tanımlamıştır ve doğal olarak bu limite onun ismi verilmiştir.




